6ES7307-1BA01-0AA0大量现货
- 供应商
- 浔之漫智控技术（上海）有限公司
- 认证
- 品牌
- 西门子
- 型号
- 模块
- 产地
- 德国
- 联系电话
- 15821971992
- 全国服务热线
- 15821971992
- 经理
- 聂聪
- 所在地
- 上海市松江区广富林路4855弄88号3楼
- 更新时间
- 2023-10-26 04:00
| 电场：凡是有电荷的地方，四周就存在着电场，即任何电荷都在自己周围的空间激发电场；而电场对于处于其中的任何其他电荷都有作用力。电荷之间的相互作用就是通过电场（一种特殊的物质）而进行的。用一个图式来概括则为： |
电荷<-->电场<-->电荷 |
| 电场强度的定义：电场中某场点上的电场强度等于置于该点的单位正电荷所受的电力. 定义式为: |
 |
电场强度叠加原理：如果以f1、f2、…、fk分别表示点电荷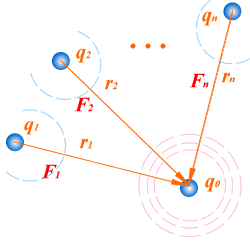 q1、q2、…、qk单独存在时电场施于空间同一点上试探电荷q0的力，则它们同时存在时，电场施于该点试探电荷的力f将为f1、f2、…、fk的矢量和，即:f=f1+f2+…+fk;将上式除以q0，我们得到:e=e1+e2+…+ek.式中e1=f1/q0，e2=f2/q0，….，ek=fk/q0分别代表q1、q2、…、qk单独存在时在空间同一点的场强，而e=f/q0代表它们同时存在时该点的总场强。 由此可见， 点电荷组所产生的电场在某点的场强等于各点电荷单独存在时所产生的电场在该点场强的矢量叠加。这叫做电场强度叠加原理（简称场强叠加原理）。 几种典型电荷的电场强度 1. 点电荷的电场强度 |
 |
| 证明： 在场点放置一个静止试探电荷q，则q受到的电场力为： |
 |
| 根据定义式 |
|
| 则 |
|
| 点电荷系的电场强度表达式为 : |
 |
| 连续分布的体电荷的电场强度: |
 ρe为电荷的体密度。 |
| 连续分布的面电荷的电场强度 : |
 σe为电荷的面密度 |
| 连续分布的线电荷的电场强度: |
 ηe为电荷的线密度。 |
高斯定理是一条反映静电场规律的普遍定理，在进一步研究电学时，这条定理很重要。在这里，我们只应用它来计算某些对称带电体所激发的电场中的场强，在这些情况中，它比应用电场强度叠加原理来计算场强要方便得多。下面举例说明高斯定理的这种应用。（1）在电场强度已知时，求出任意区域内的电荷（2）当电荷分布具有某种特殊对称性时，用高斯定理求出该种电荷系统的电场分布 例1：求均匀带正电球体内外的电场分布，设球体带电量为q，半径为r。应用电通量的定义和高斯定理联立求解。(解略)讨论：在球面外(r>r)，点p的场强为: 方向沿半径指向球外(如q<0，则沿半径指向球内)。 在球面内(r<r),点p的场强为:，可得如下结论：均匀带电球面外的场强，与将球面上电荷全部集中于中心的点电荷所激发的场强一样；球面内任一点的场强则为零。均匀带电球面的场强分布，可用其大小e与距离r的关系曲线来表示。这条曲线e-r在r=r处是间断的，即场强大小e的分布在该处是不连续的。例2：均匀带正电无限长细棒的场强.其线电荷密度为.场强的大小为：例3：均匀带正电的无限大平面薄板的场强。 |